Hola amigos. Muchos de nosotros, compramos puzzles descatalogados usados. Rarezas puzzleras y antigüedades, que fuera del mercado de segunda mano son improbables de adquirir. Con ellos es imposible saber de entrada si están completos, por mucho que el vendedor nos garantice su integridad. Podemos hacer el recuento pieza a pieza, pero es muy fácil equivocarse y caer en el error. Con puzzles pequeños, podemos repetir la cuenta un par o tres de veces para asegurar el resultado. Pero es de locos utilizar ese sistema en puzzles de mediano o gran tamaño. A continuación os explico como resolver ese problema sin demasiado esfuerzo. Procuraré resumirlo de manera esquemática y entendedora.
El primer paso es separar las piezas de ángulo recto y enlazar el marco. Debemos asegurarnos de hacer esta primera selección de manera correcta. Si ya de entrada nos falta alguna pieza empezamos mal el asunto. Aunque si eso ocurre, deberemos tener en cuenta las piezas perdidas para hacer el cálculo. Pero supongamos que el recuadro está entero. Haremos entonces la multiplicación de la base por la altura para saber con precisión el número de piezas exactas que componen el rompecabezas. Un puzzle no tiene por qué tener el mismo número de piezas que el número de piezas que marca su descripción. El redondeo al alza lo hacen las marcas con fines comerciales. Imaginemos pues que tenemos un puzzle de 6000 piezas, por ejemplo. En la base nos salen 81 piezas, mientras que la altura se compone de 74. Aquí no hay que ser experto en matemáticas, para entender que obtendremos la exactitud de piezas al multiplicar 81×74=5994 piezas. Podemos ahora demandar a la marca por publicidad engañosa y seguir con nuestras operaciones.
Debo aclarar que las cifras dadas aquí son meramente orientativas. Dependerá de la estructura interna de cada puzzle de que salgan unos números u otros diferentes. Y si bien es cierto que hemos dedicado ya un tiempo considerable sin llegar a ninguna conclusión, la parte que supondrá un alivio para nuestra mente será la siguiente.
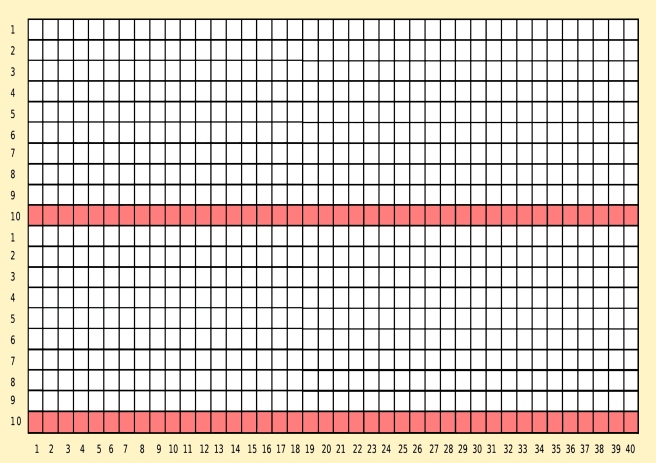
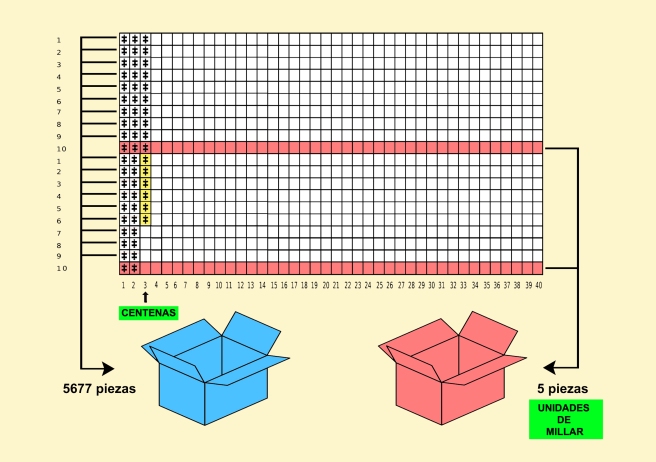
Se trata de utilizar una cuadrícula del tamaño que queramos y marcar de alguna manera la décima casilla de cada columna. Esto se puede hacer sobre un cartón o una madera y del modo que seamos más ingeniosos. En nuestro ejemplo, emplearemos una lámina madera de 140 cm x 70 cm que dividiremos en 40 casillas verticales y 20 horizontales. Nos saldrán un total de 800 casillas de 3,5 cm². Las diez primeras hileras verticales corresponderán a una primera serie de diez y las diez segundas a una segunda serie, también de diez. Debe quedar muy claro que lo que estamos haciendo es duplicar el patrón para agilizar los números. Lo importante es que la sucesión de piezas sea con base 10 y dependerá de cada persona las dimensiones a elegir. Cuanto mayor sea la capacidad del encasillado, menos veces habrá que repetir el procedimiento.
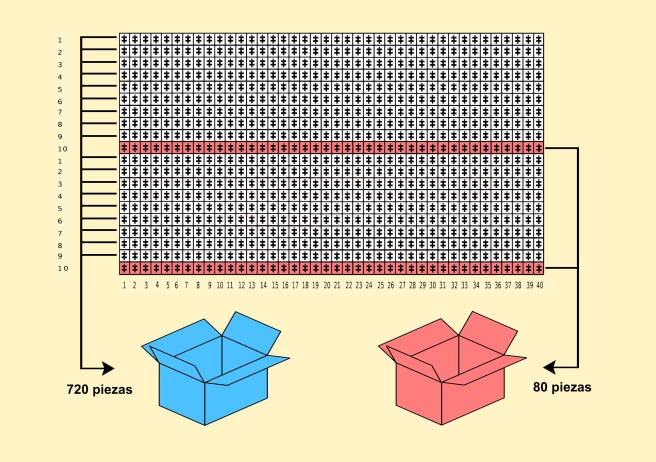
Debemos entonces llenar la plantilla de piezas, una por casilla, sin preocuparnos de contar. El tablero segmentado ya actúa por si solo de marcador. Una vez todas colocadas, hay que retirar las piezas que ocupan la décima casilla de todas las columnas verticales, que hemos señalado en rojo, y agruparlas en una caja aparte, roja también. Tiene que haber 80 piezas si hemos hecho lo correcto, que tampoco nos molestamos en contar. El resto de piezas, que ya no volveremos a necesitar, las guardamos en una caja diferente, que nosotros hemos definido como azul.
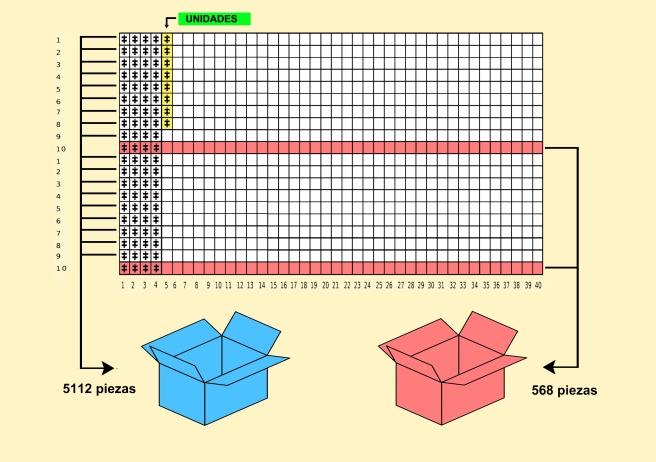
Repetimos el proceso tantas veces como seamos capaces de llenar la tabla. En nuestro caso, al dividir 5994 entre 800, nos da como resultado que tendremos que repetir la pauta 7 veces. Pero en la octava secuencia, situaremos las piezas igualmente por ringleras hasta llegar a una quinta columna, señalada en amarillo, en la que solo podremos poner 8 piezas. Ese 8, serán las unidades,que una vez descifradas, desecharemos también al montón de piezas de la caja azul.
Nosotros que hemos hecho los cálculos, sabemos que en esa caja hay ahora un total de 5112 piezas. Pero ese es un dato anecdótico, que en su momento desconoceremos y no nos supondrá obstáculo alguno para hallar la cuantía defintiva. Nos sirve solo para dejar constancia, de lo que supondría para nuestra sesera contar tal cantidad de piezas de una en una.
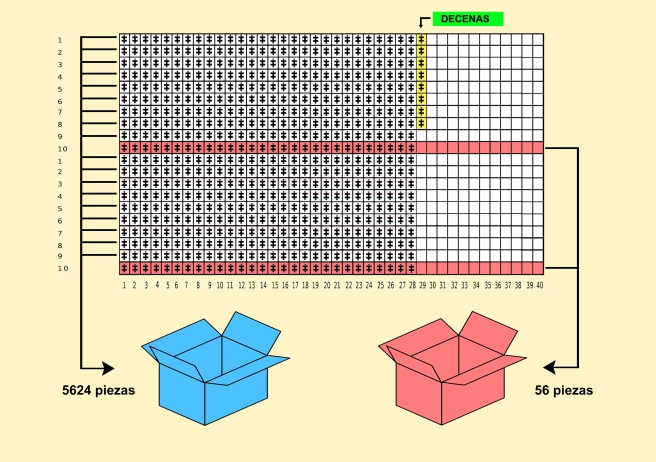
Con las casillas del tablero otra vez vacías, repetimos la pauta pero utilizando exclusivamente las piezas que hemos acumulado en la caja roja. Tendría que haber 568 piezas, que tampoco nos detendremos a contar. Podremos ocupar con ellas 28 hileras enteras y nos volverán a quedar 8 piezas libres en la columna 29. Ese nuevo 8 lo asociaremos a las decenas. Nos quedaremos de nuevo con las piezas ubicadas en las décimas casillas, descartando las demás, que serán almacenadas con las ya desechadas anteriormente.
Tendremos ahora solamente 56 piezas en nuestro haber y procederemos a realizar otro reparto. Podremos rellenar 2 filas enteras y parte una tercera. La otra parte de esta tercera columna, corresponderá a una nueva serie decimal en la que únicamente podremos colocar 6 piezas. El 6 pues, será la cifra referida a las centenas. Y para averiguar el número correspondiente a las unidades de millar,no nos queda otro que el 5, que serán las 5 piezas que ocupan las 5 casillas rojas que hemos podido rellenar. Así que… !voilà! ya tenemos un número ganador: El 5688.
Pero ese número no será el número de piezas definitivo, ya que todavía debemos sumar las piezas del marco. Dijimos que teníamos 81 piezas por lado horizontal más 74 piezas por lado vertical. Así que la suma total de las piezas del perímetro será de 81+81+72 +72=306 (Sumamos 72 en vez de 74, porqué debemos restar 2 dígitos por número para no repetir las dos piezas ya incluidas dentro del 81). Esa cantidad hay que sumarla al cómputo de piezas que teníamos hasta el momento y obtendremos el resultado final: 5688 + 306 = 5994. Comprovamos que nos sale la misma cantidad de piezas que en la multiplicación inicial, con lo que ahora sí podemos afirmar con absoluta certeza que el puzzle está completo. Si el resultado es menor, sabremos también con seguridad que nos faltan piezas y nos han vendido un producto defectuoso.
Y hasta aquí este sencillo ejercicio de aritmética. Puede que en algún momento resulte algo confuso si somos más bien de letras que de ciencias. Pero os garantizo que es una manera rápida de calcular y evitaréis futuros quebraderos de cabeza. Espero haber servido de ayuda a alguien. Saludos.